OWL ontology is a set of axioms, which provide explicit logical assertions about three types of things - classes, individuals and properties. By using a piece of software called a reasoner we can infer other facts which are implicitly contained in the ontology, for example if an individual Martin is in class Student, and the class Student is a subclass of the class Person, a reasoner will infer that Martin is a Person.
There are two types of properties in OWL ontologies. Data properties are binary relations that link an individual to a piece of typed data, like to an xsd:dateTime or xsd:string literal. Object properties are binary relations that link an individual to an individual.
There are many ways how an OWL ontology can be written, however the important thing is the ontology meaning, which can be shown in a picture. I use here the Ontograf images produced by Protege OWL editor. For example, here is a small ontology with two classes and an individual, which has one data property:
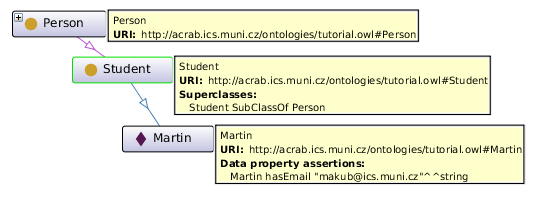
The same axiom can be written in several ways. The most common is the XML/RDF format, the OWL 2 specification uses the functional syntax format, the Protege authors developed a shorter Manchester format, and the most concise format is Turtle. I will use the functional syntax format in this tutorial, and in some cases I will show also the Manchester syntax when it is more understandable.
Class declaration defines a class. A class may contain individuals.

|
Declaration( Class( :Person ) ) |
Individual declaration defines a named individual.

|
Declaration( NamedIndividual( :Martin ) ) |
Class assertion state that an individual belongs to a class:

|
ClassAssertion( :Student :Martin ) |
Subclass assertion declares that all individuals that belong to a class belong also to another class.
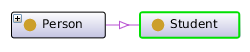
|
SubClassOf( :Student :Person ) |
Property declaration defines either a data property to link an individual to data, or object property to link to an individual:
|
Declaration( DataProperty( :hasEmail ) ) Declaration( ObjectProperty( :hasSpouse ) ) |
Property assertion states the relation of an individual to either data or individual:

|
DataPropertyAssertion( :hasEmail :Martin "makub@ics.muni.cz"^^xsd:string ) ObjectPropertyAssertion( :hasSpouse :Martin :Lenka ) |
Negative property assertion states that the relation of an individual to either data or individual does not exist. OWL uses Open World Assumption, so if an individual is not linked by some property with some value, it may be caused by two reasons - either it really does not have the property with the value, or it is unknown because the information missing from the ontology. A negative property assertion states that the individual cannot possibly have that property value.
NegativeObjectPropertyAssertion( :hasSpouse :Martin :Peter) NegativeDataPropertyAssertion( :hasEmail :Martin "president@whitehouse.gov")
Annotation assertion enables to annotate anything with some details, for example we may use ICS as the name of an individual because it is an abbreviation, and use annotation to label the abbreviation with the full meaning "Institute of Computer Science". The images generated by Protege then show the label instead of the name.

|
Declaration( NamedIndividual( :MU )) AnnotationAssertion( rdfs:label :MU "Masaryk University" ) Declaration( NamedIndividual( :ICS ) ) AnnotationAssertion( rdfs:label :ICS "Institute of Computer Science" ) Declaration( NamedIndividual(:SC) ) AnnotationAssertion( rdfs:label :SC "Supercomputing Center" ) |
We can define many things about properties (see OWL 2 Syntax - Object Property Axioms and OWL2 Direct Semantic - Object Property Expression Axioms for details), that a property is transitive, symmetric, asymmetric, reflexive, irreflexive, functional (can have only one value), inverse-functional (its inverse is functional), inverse to some other property, subproperty of some other property, equivalent to some other property, or disjoint with some other property (two individuals cannot be linked by both properties in the same time).
In a simple example, we can define that the property hasSpouse is symmetric, functional and irreflexive:
|
SymmetricObjectProperty( :hasSpouse ) FunctionalObjectProperty( :hasSpouse ) IrreflexiveObjectProperty( :hasSpouse ) |
In a more elaborate example, in the following image, a new transitive property isPartOf is defined, which connects the organizational parts of Masaryk University. Then the property hasPart is defined as an inverse property to isPartOf.

|
Declaration( ObjectProperty( :isPartOf )) TransitiveObjectProperty( :isPartOf ) ObjectPropertyAssertion( :isPartOf :SC :ICS ) ObjectPropertyAssertion( :isPartOf :ICS :MU ) Declaration( ObjectProperty(:hasPart) ) InverseObjectProperties( :hasPart :isPartOf ) |
Now we can use a reasoner to infer the other properties. Because the isPartOf is transitive, SCB isPartOf MU, and because hasPart is inverse to isPartOf, we get the complete inferred relations:
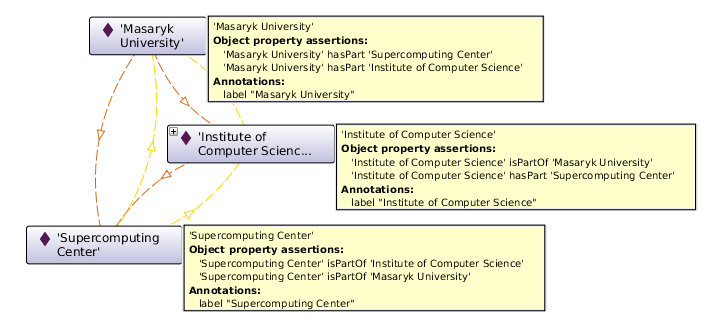
|
ObjectPropertyAssertion( :isPartOf :SC :MU ) ObjectPropertyAssertion( :hasPart :MU :SC ) ObjectPropertyAssertion( :hasPart :MU :ICS ) ObjectPropertyAssertion( :hasPart :ICS :SC ) |
It shows the power of reasoning - we do not have to declare all relations, just the needed minimum, and the rest can be inferred.
The version 2 of OWL introduced important new feature - chained properties. They allow to define some relationships among three individuals, the most prominent example is the property uncle which may be defined as chain of parent and brother properties.
A property may be chained even with itself. For example, we may define property isEmployedAt, which is a chain of itself and the transitive property isPartOf, meaning that if a person is imployed at some organizational unit, the person is also employed at the bigger organizational units.
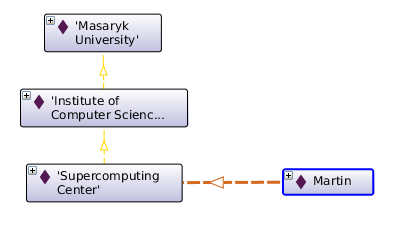
|
Declaration( ObjectProperty( :isEmployedAt ) ) ObjectPropertyAssertion( :isEmployedAt :Martin :SC ) SubObjectPropertyOf( ObjectPropertyChain( :isEmployedAt :isPartOf ) :isEmployedAt) |
Again, using a reasoner we may infer the complete relations:
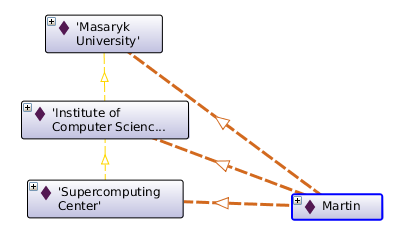
|
ObjectPropertyAssertion( :isEmployedAt :Martin :ICS ) ObjectPropertyAssertion( :isEmployedAt :Martin :MU ) |
Classes may be defined using class expressions. (For details, see OWL 2 Syntax - Class expressions and OWL 2 Direct Semantics - Class Expression Axioms.) A common class definition is an assertion that a named class is equivalent to some (unnamed/anonymous) class defined by an expression. Classes can also be defined as disjoined with other class which means that they do not share any individuals.
OWL 2 provides set operations in their usual mathematical meaning.
Let's show the set operations on an example. We can define a new class Child which contains four new individuals named SmallBoy, BigBoy, SmallGirl, BigGirl. These individuals must be declared as different from each other, otherwise an OWL reasoner expects that they may be the same:
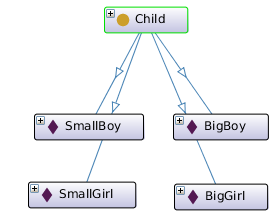
|
Declaration( Class( :Child ) ) Declaration( NamedIndividual( :BigBoy ) ) Declaration( NamedIndividual( :BigGirl ) ) Declaration( NamedIndividual( :SmallBoy ) ) Declaration( NamedIndividual( :SmallGirl ) ) ClassAssertion( :Child :BigBoy ) ClassAssertion( :Child :BigGirl ) ClassAssertion( :Child :SmallBoy ) ClassAssertion( :Child :SmallGirl ) DifferentIndividuals( :BigBoy :BigGirl :SmallBoy :SmallGirl ) |
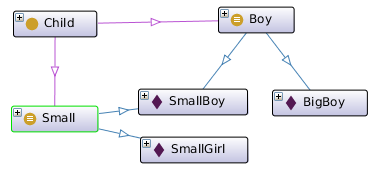
Let's define two base classes by enumerating their members, the Boy class containing boys and the Small class containing the small children. I.e. the individual SmallBoy is both in Boy and in Small classes. Here the functional syntax is not as nice as the Manchester syntax used in the Protege OWL editor, so both syntaxes are shown:
|
functional syntax:
SubClassOf(:Boy :Child) SubClassOf(:Small :Child) EquivalentClasses(:Boy ObjectOneOf(:SmallBoy :BigBoy)) EquivalentClasses(:Small ObjectOneOf(:SmallBoy :SmallGirl)) |
Manchester syntax:
Class: Boy
EquivalentTo:
{BigBoy , SmallBoy}
SubClassOf:
Child
Class: Small
EquivalentTo:
{SmallBoy , SmallGirl}
SubClassOf:
Child
|
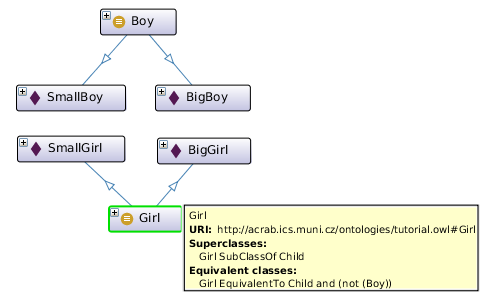
Now we can define a new class Girl as a class that is the intersection of the class Child with an unnamed class that is the complement of the class Boy. This is a bit complicated description, the same is more intuitive in the Protege/Manchester format, where Girl class is equivalent to Child and not Boy, i.e. a girl is a child that is not a boy.
With such definition, a reasoner will find that the Girl class contains the individuals SmallGirl and BigGirl.
|
functional syntax:
Declaration( Class( :Girl ) ) SubClassOf( :Girl :Child ) EquivalentClasses( :Girl ObjectIntersectionOf( ObjectComplementOf( :Boy ) :Child ) )Protege syntax:
Class: Girl
SubClassOf:
Child
EquivalentTo:
Child and (not (Boy))
|
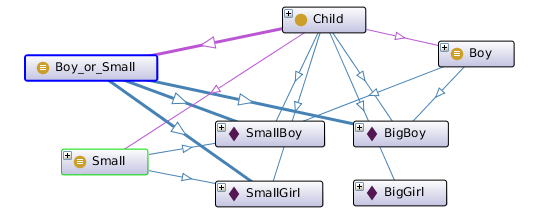
We can define a new class Boy_or_small as the union of the classes Small and Boy. Again, the description is more intuitive in the Protege syntax as Boy or Small. A reasoner will find that the class contains the individuals SmallBoy, SmallGirl, BigBoy:
|
functional syntax:
Declaration( Class( :Boy_or_Small ) ) EquivalentClasses( :Boy_or_Small ObjectUnionOf( :Small :Boy ) )Protege syntax:
Class: Boy_or_Small
EquivalentTo:
Boy
or Small
|
A class expression can say that the class contains only individuals that are connected by a given property with individuals from a given class. Let's show it on an example. We may define a new class OrgUnit which contains the three individuals MU, ICS, SC.
Declaration( Class( :OrgUnit )) ClassAssertion( :OrgUnit :ICS ) ClassAssertion( :OrgUnit :MU ) ClassAssertion( :OrgUnit :SC )
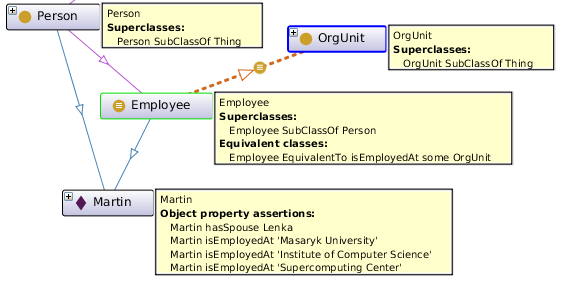
Then we may define a new class Employee as a subclass of Person, which is equivalent to an anonymous class of individuals that are linked by property isEmployedAt to individuals from the class OrgUnit. The meaning is that employees are the persons that are employed somewhere:

|
functional syntax:
Declaration( Class( :Employee) ) SubClassOf( :Employee :Person ) EquivalentClasses( :Employee ObjectSomeValuesFrom( :isEmployedAt :OrgUnit ) )Protege syntax:
Class: Employee
SubClassOf:
Person
EquivalentTo:
isEmployedAt some OrgUnit
|
By using a reasoner we may infer that the class Employee contains the individual Martin. The reasoner may even produce an explanation for this:
|
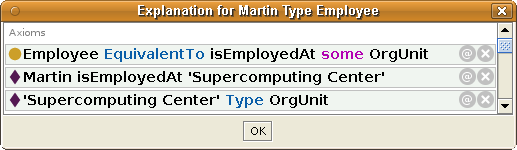
|
A class expression can also say that the class contains individuals that are connected by a given property with a given individual.
In our example, we can define a new class EmployeesOfMU as containing individuals that are connected by the property isEmployedAt with the individual MU, i.e. as those who are employed at MU. A reasoner will find that the class contains the individual Martin.
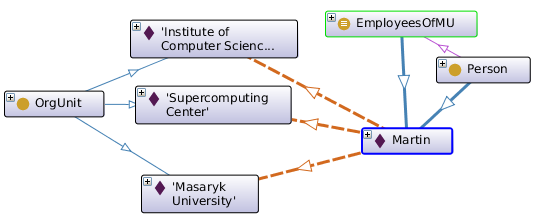
|
functional syntax:
Declaration( Class( :EmployeesOfMU ) ) SubClassOf( :EmployeesOfMU :Person ) EquivalentClasses( :EmployeesOfMU ObjectHasValue( :isEmployedAt :MU ) )Protege syntax:
Class: EmployeesOfMU
SubClassOf:
Person
EquivalentTo:
isEmployedAt value MU
|
Universal quantification (in mathematics known by the operator ∀) in OWL is a bit odd because of the open world assumption that OWL has.
The existential quantification described above (OWL operator ObjectSomeValuesFrom()) as defined in
OWL 2 Direct Semantics states
"individuals such that there exists some individual from the given class connected by the given property",
in mathematical notation ObjectSomeValuesFrom( OPE CE ) : { x | ∃ y : ( x, y ) ∈ (OPE)OP and y ∈ (CE)C }
where OPE denotes an object property expression, .OP is object property interpretation function,
CE denotes a class expression, .C is class interpretation function.
The universal quantification is defined as operator ObjectAllValuesFrom( OPE CE ) : { x | ∀ y : ( x, y ) ∈ (OPE)OP implies y ∈ (CE)C } which means individuals such that they are always connected by the given property only to individuals from the given class.
The problem with open world assumption is that in the open world an ontology may not contain all information. For example, imagine an ontology that states that the individual Peter has two children, sons John and Paul. We may define a class ManWhoHaveOnlySons as the class of individuals that are connected by property hasChild only to individuals from the class Boy, i.e. ObjectAllValuesFrom( :hasChild :Boy). However the individual Peter is not necessarily in the class, because Peter may also have a daughter Jane, just the ontology does not contain this information.
Universal quantification in OWL works only together with cardinality restrictions, so that if we know that an individual can be connected by a given property to at most some number of different individuals, and we know all the individuals, then a conclusion can be drawn.
It is a bit hard to find an example in real life, but here is one. Every person has at most two parents. Let's say that if both parents are of the same nationality, then the person has the same nationality.
Let's create a new individual Ivan, which is connected by a new object property hasParent to the individuals Martin and Lenka. The meaning is that Ivan is a child of Martin and Lenka.
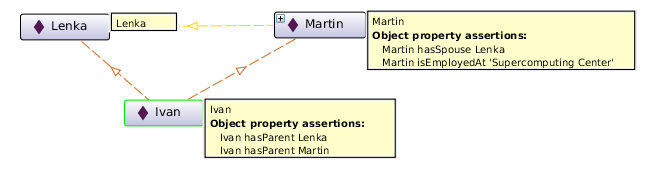
|
Declaration( NamedIndividual( :Ivan ) ) ClassAssertion( :Person :Ivan ) Declaration( ObjectProperty( :hasParent ) ) ObjectPropertyAssertion( :hasParent :Ivan :Martin ) ObjectPropertyAssertion( :hasParent :Ivan :Lenka ) |
We can state that a Person has at most two parents, and define a new class Czech containing Martin and Lenka. The important new thing are the last two axioms - the universal quantification that individuals that have all parents Czech are (a subclass of) Czechs, and that all named individuals in our ontology are different:
SubClassOf( :Person ObjectMaxCardinality( 2 :hasParent ) ) Declaration( Class( :Czech ) ) SubClassOf( :Czech :Person ) ClassAssertion( :Czech :Lenka ) ClassAssertion( :Czech :Martin ) SubClassOf( ObjectAllValuesFrom( :hasParent :Czech ) :Czech) DifferentIndividuals( :BigBoy :BigGirl :ICS :Ivan :Lenka :MU :Martin :SC :SmallBoy :SmallGirl)
With these axioms, the conclusion made by a reasoner is - Ivan is in the class Czech. He is a Person, so he can have at most two parents, he does have two parents which are different individuals, and both are Czech. Thus no more parents can exist for him, and the universal quantificator can be satistied - he has only Czech parents.
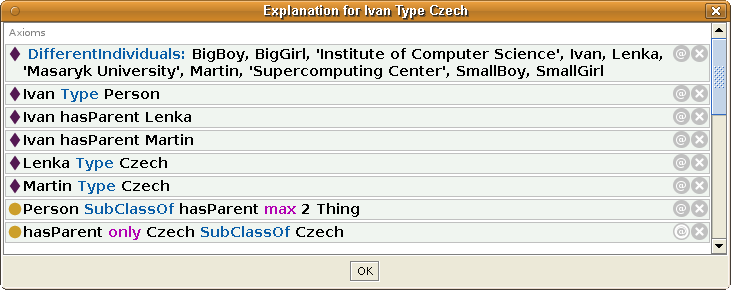
EquivalentClasses( :Person DataExactCardinality( 1 :hasAge DatatypeRestriction( xsd:integer xsd:minInclusive "0"^^xsd:integer xsd:maxInclusive "130"^^xsd:integer)))or in the Manchester syntax
Class: Person
EquivalentTo:
hasAge exactly 1 xsd:integer[>= 0 , <= 130]
defines that individuals in the Person class have exactly one value of the hasAge property that is an integer in the range between 0 and 130.
The OWL 2 language is not able to express all relations. One know example is that it cannot express the relation child of married parents, because there is no way in OWL 2 to express the relation between individuals with which an individual has relations.
The expresivity of OWL can be extended by adding SWRL (Semantic Web Rule Language) rules to an ontology. SWRL rules are similar to rules in Prolog or DATALOG languages. In fact, SWRL rules are DATALOG rules with unary predicates for describing classes and data types, binary predicates for properties, and some special built-in n-ary predicates. (See the section SWRL predicates for details)
Protege OWL editor supports SWRL rules, and the reasoners Pellet and Hermit also support SWRL rules.
Let's reuse our example of Ivan, the son of Martin and Lenka. The symmetric property hasSpouse connects Martin and Lenka.

|
SymmetricObjectProperty(:hasSpouse) ObjectPropertyAssertion(:hasSpouse :Martin :Lenka) ObjectPropertyAssertion( :hasParent :Ivan :Martin ) ObjectPropertyAssertion( :hasParent :Ivan :Lenka ) |
Person(?x), hasParent(?x, ?y), hasParent(?x, ?z), hasSpouse(?y, ?z) -> ChildOfMarriedParents(?x)It can be described in functional syntax too:
Prefix(var:=<urn:swrl#>)
Declaration( Class( :ChildOfMarriedParents ) )
SubClassOf( :ChildOfMarriedParents :Person )
DLSafeRule(
Body(
ClassAtom( :Person Variable(var:x))
ObjectPropertyAtom( :hasParent Variable(var:x) Variable(var:y) )
ObjectPropertyAtom( :hasParent Variable(var:x) Variable(var:z) )
ObjectPropertyAtom( :hasSpouse Variable(var:y) Variable(var:z) )
)
Head(
ClassAtom( :ChildOfMarriedParents Variable(var:x) )
)
)
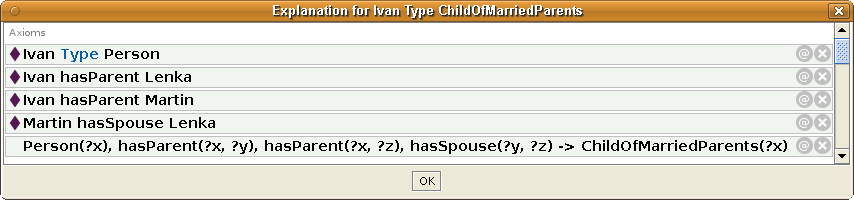
When we use the Pellet or Hermit reasoner that supports SWRL rules, it infers that Ivan belongs to the class ChildOfMarriedParents, and even explains why:
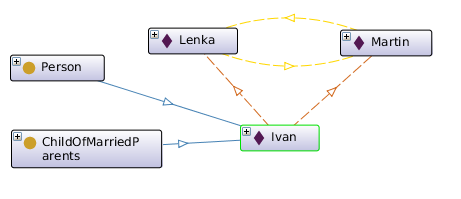
|
ClassAssertion( :ChildOfMarriedParents :Ivan ) |
The OWL's open world assumption says that an ontology may not contain all information and thus some information may be unknown. This is why named individuals with different names may represent the same individual unless it is explicitely stated that they are different. This is also why we had to specify in the examples above (the set operations and the universal quantification) that the individuals are different.
We can declare the named individuals different in two ways. One is by the DifferentIndividuals() axiom:
DifferentIndividuals(:BigBoy :BigGirl :SmallBoy :SmallGirl :ICS :MU :SC :Ivan :Lenka :Martin )
However this way is known to cause performance problems for reasoner when the number of individuals is large. The second way how to make individuals different is to use a functional data property with unique values. Functional property can have only one value, and thus makes individuals different when their values are different. If the property is also declared as a key, it makes individuals with the same value to be the same individual.
Declaration(DataProperty(:hasId)) FunctionalDataProperty(:hasId) HasKey( :Person () (:hasId) ) DataPropertyAssertion(:hasId :Lenka "1234") DataPropertyAssertion(:hasId :Martin "5648")
An ontology is not of much value if it is not used. Fortunately there are already tools for using an ontology in your programming code. I recommend using the following tools:
I have prepared a Maven project that contains all the sources from this example, dependencies on OWL API from Maven Central repository, and Pellet 2.2 from Berkeley BOP Maven Repository. The Maven project can be compiled and used either from a command line, or from an integrated development environment like IntelliJ IDEA, Eclipse or NetBeans.
Update 2015-02-25: OWL API has moved to https://github.com/owlcs/owlapi/ and Protege 5 is using newer OWL API 4
Update 2016-05-06: I have updated the code examples in the gitHub repository to OWL API 4.2.3
Clone the Git repository https://github.com/martin-kuba/owl2-swrl-tutorial.
There are examples how to use OWL API, however I show here my own:
package cz.makub; import com.clarkparsia.owlapi.explanation.DefaultExplanationGenerator; import com.clarkparsia.owlapi.explanation.util.SilentExplanationProgressMonitor; import com.clarkparsia.pellet.owlapiv3.PelletReasonerFactory; import org.semanticweb.owlapi.apibinding.OWLManager; import org.semanticweb.owlapi.io.OWLObjectRenderer; import org.semanticweb.owlapi.model.*; import org.semanticweb.owlapi.reasoner.OWLReasoner; import org.semanticweb.owlapi.reasoner.OWLReasonerFactory; import org.semanticweb.owlapi.reasoner.SimpleConfiguration; import org.semanticweb.owlapi.vocab.OWLRDFVocabulary; import org.semanticweb.owlapi.vocab.PrefixOWLOntologyFormat; import uk.ac.manchester.cs.bhig.util.Tree; import uk.ac.manchester.cs.owl.explanation.ordering.ExplanationOrderer; import uk.ac.manchester.cs.owl.explanation.ordering.ExplanationOrdererImpl; import uk.ac.manchester.cs.owl.explanation.ordering.ExplanationTree; import uk.ac.manchester.cs.owlapi.dlsyntax.DLSyntaxObjectRenderer; import java.util.*; /** * Example how to use an OWL ontology with a reasoner. * * Run in Maven with <code>mvn compile; mvn exec:java -Dexec.mainClass=cz.makub.Tutorial</code> * * @author Martin Kuba makub@ics.muni.cz */ public class Tutorial { private static final String BASE_URL = "http://acrab.ics.muni.cz/ontologies/tutorial.owl"; private static OWLObjectRenderer renderer = new DLSyntaxObjectRenderer(); public static void main(String[] args) throws OWLOntologyCreationException { //prepare ontology and reasoner OWLOntologyManager manager = OWLManager.createOWLOntologyManager(); OWLOntology ontology = manager.loadOntologyFromOntologyDocument(IRI.create(BASE_URL)); OWLReasonerFactory reasonerFactory = PelletReasonerFactory.getInstance(); OWLReasoner reasoner = reasonerFactory.createReasoner(ontology, new SimpleConfiguration()); OWLDataFactory factory = manager.getOWLDataFactory(); PrefixOWLOntologyFormat pm = (PrefixOWLOntologyFormat) manager.getOntologyFormat(ontology); pm.setDefaultPrefix(BASE_URL + "#"); //get class and its individuals OWLClass personClass = factory.getOWLClass(":Person", pm); for (OWLNamedIndividual person : reasoner.getInstances(personClass, false).getFlattened()) { System.out.println("person : " + renderer.render(person)); } //get a given individual OWLNamedIndividual martin = factory.getOWLNamedIndividual(":Martin", pm); //get values of selected properties on the individual OWLDataProperty hasEmailProperty = factory.getOWLDataProperty(":hasEmail", pm); OWLObjectProperty isEmployedAtProperty = factory.getOWLObjectProperty(":isEmployedAt", pm); for (OWLLiteral email : reasoner.getDataPropertyValues(martin, hasEmailProperty)) { System.out.println("Martin has email: " + email.getLiteral()); } for (OWLNamedIndividual ind : reasoner.getObjectPropertyValues(martin, isEmployedAtProperty).getFlattened()) { System.out.println("Martin is employed at: " + renderer.render(ind)); } //get labels LocalizedAnnotationSelector as = new LocalizedAnnotationSelector(ontology, factory, "en", "cs"); for (OWLNamedIndividual ind : reasoner.getObjectPropertyValues(martin, isEmployedAtProperty).getFlattened()) { System.out.println("Martin is employed at: '" + as.getLabel(ind) + "'"); } //get inverse of a property, i.e. which individuals are in relation with a given individual OWLNamedIndividual university = factory.getOWLNamedIndividual(":MU", pm); OWLObjectPropertyExpression inverse = factory.getOWLObjectInverseOf(isEmployedAtProperty); for (OWLNamedIndividual ind : reasoner.getObjectPropertyValues(university, inverse).getFlattened()) { System.out.println("MU inverseOf(isEmployedAt) -> " + renderer.render(ind)); } //find to which classes the individual belongs Set<OWLClassExpression> assertedClasses = martin.getTypes(ontology); for (OWLClass c : reasoner.getTypes(martin, false).getFlattened()) { boolean asserted = assertedClasses.contains(c); System.out.println((asserted ? "asserted" : "inferred") + " class for Martin: " + renderer.render(c)); } //list all object property values for the individual Map<OWLObjectPropertyExpression, Set<OWLIndividual>> assertedValues = martin.getObjectPropertyValues(ontology); for (OWLObjectProperty objProp : ontology.getObjectPropertiesInSignature(true)) { for (OWLNamedIndividual ind : reasoner.getObjectPropertyValues(martin, objProp).getFlattened()) { boolean asserted = assertedValues.get(objProp).contains(ind); System.out.println((asserted ? "asserted" : "inferred") + " object property for Martin: " + renderer.render(objProp) + " -> " + renderer.render(ind)); } } //list all same individuals for (OWLNamedIndividual ind : reasoner.getSameIndividuals(martin)) { System.out.println("same as Martin: " + renderer.render(ind)); } //ask reasoner whether Martin is employed at MU boolean result = reasoner.isEntailed(factory.getOWLObjectPropertyAssertionAxiom(isEmployedAtProperty, martin, university)); System.out.println("Is Martin employed at MU ? : " + result); //check whether the SWRL rule is used OWLNamedIndividual ivan = factory.getOWLNamedIndividual(":Ivan", pm); OWLClass chOMPClass = factory.getOWLClass(":ChildOfMarriedParents", pm); OWLClassAssertionAxiom axiomToExplain = factory.getOWLClassAssertionAxiom(chOMPClass, ivan); System.out.println("Is Ivan child of married parents ? : " + reasoner.isEntailed(axiomToExplain)); //explain why Ivan is child of married parents DefaultExplanationGenerator explanationGenerator = new DefaultExplanationGenerator( manager, reasonerFactory, ontology, reasoner, new SilentExplanationProgressMonitor()); Set<OWLAxiom> explanation = explanationGenerator.getExplanation(axiomToExplain); ExplanationOrderer deo = new ExplanationOrdererImpl(manager); ExplanationTree explanationTree = deo.getOrderedExplanation(axiomToExplain, explanation); System.out.println(); System.out.println("-- explanation why Ivan is in class ChildOfMarriedParents --"); printIndented(explanationTree, ""); } private static void printIndented(Tree<OWLAxiom> node, String indent) { OWLAxiom axiom = node.getUserObject(); System.out.println(indent + renderer.render(axiom)); if (!node.isLeaf()) { for (Tree<OWLAxiom> child : node.getChildren()) { printIndented(child, indent + " "); } } } /** * Helper class for extracting labels, comments and other anotations in preffered languages. * Selects the first literal annotation matching the given languages in the given order. */ public static class LocalizedAnnotationSelector { private final List<String> langs; private final OWLOntology ontology; private final OWLDataFactory factory; /** * Constructor. * * @param ontology ontology * @param factory data factory * @param langs list of prefered languages; if none is provided the Locale.getDefault() is used */ public LocalizedAnnotationSelector(OWLOntology ontology, OWLDataFactory factory, String... langs) { this.langs = (langs == null) ? Arrays.asList(Locale.getDefault().toString()) : Arrays.asList(langs); this.ontology = ontology; this.factory = factory; } /** * Provides the first label in the first matching language. * * @param ind individual * @return label in one of preferred languages or null if not available */ public String getLabel(OWLNamedIndividual ind) { return getAnnotationString(ind, OWLRDFVocabulary.RDFS_LABEL.getIRI()); } @SuppressWarnings("UnusedDeclaration") public String getComment(OWLNamedIndividual ind) { return getAnnotationString(ind, OWLRDFVocabulary.RDFS_COMMENT.getIRI()); } public String getAnnotationString(OWLNamedIndividual ind, IRI annotationIRI) { return getLocalizedString(ind.getAnnotations(ontology, factory.getOWLAnnotationProperty(annotationIRI))); } private String getLocalizedString(Set<OWLAnnotation> annotations) { List<OWLLiteral> literalLabels = new ArrayList<OWLLiteral>(annotations.size()); for (OWLAnnotation label : annotations) { if (label.getValue() instanceof OWLLiteral) { literalLabels.add((OWLLiteral) label.getValue()); } } for (String lang : langs) { for (OWLLiteral literal : literalLabels) { if (literal.hasLang(lang)) return literal.getLiteral(); } } for (OWLLiteral literal : literalLabels) { if (!literal.hasLang()) return literal.getLiteral(); } return null; } } }
Program output:
person : BigBoy
person : Lenka
person : SmallGirl
person : SmallBoy
person : Martin
person : Ivan
person : BigGirl
Martin has email: makub@ics.muni.cz
Martin is employed at: ICS
Martin is employed at: SC
Martin is employed at: MU
Martin is employed at: 'Institute of Computer Science'
Martin is employed at: 'Supercomputing Center'
Martin is employed at: 'Masaryk University'
MU inverseOf(isEmployedAt) -> Martin
inferred class for Martin: ⊤
asserted class for Martin: Czech
inferred class for Martin: EmployeesOfMU
inferred class for Martin: Person
asserted class for Martin: Student
inferred class for Martin: Employee
asserted object property for Martin: hasSpouse -> Lenka
inferred object property for Martin: isEmployedAt -> ICS
asserted object property for Martin: isEmployedAt -> SC
inferred object property for Martin: isEmployedAt -> MU
same as Martin: Martin
Is Martin employed at MU ? : true
Is Ivan child of married parents ? : true
-- explanation why Ivan is in class ChildOfMarriedParents --
ChildOfMarriedParents(Ivan)
Person(Ivan)
hasParent(Ivan, Martin)
hasParent(Ivan, Lenka)
hasSpouse(Martin, Lenka)
ChildOfMarriedParents(?x) ← Person(?x) ⋀ hasParent(?x, ?y) ⋀ hasParent(?x, ?z) ⋀ hasSpouse(?y, ?z)
SWRL rules can use other predicates than just class or property names. The predicates can be
Let's show it on an example. A simple ontology with rules is available at swrl_tutorial.owl. It defines three individuals with their birthdays:
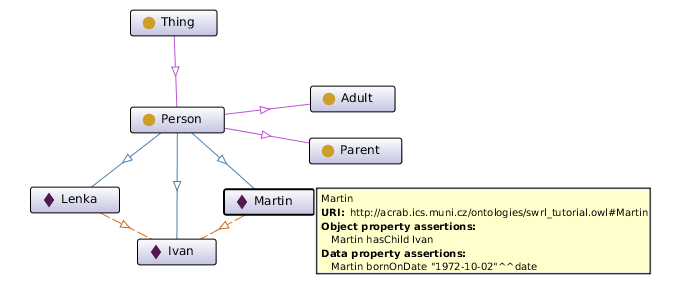
Declaration(Class(:Person)) Declaration(ObjectProperty(:hasChild)) Declaration(Class(:Parent)) Declaration(Class(:Adult)) SubClassOf(:Adult :Person) SubClassOf(:Parent :Person) Declaration(DataProperty(:bornOnDate)) Declaration(DataProperty(:bornInYear)) Declaration(DataProperty(:hasAge)) FunctionalDataProperty(:hasAge) Declaration(DataProperty(:hasDriverAge)) Declaration(NamedIndividual(:Martin)) ClassAssertion(:Person :Martin) DataPropertyAssertion(:bornOnDate :Martin "1972-10-02"^^xsd:date) Declaration(NamedIndividual(:Lenka)) ClassAssertion(:Person :Lenka) DataPropertyAssertion(:bornOnDate :Lenka "1975-11-10"^^xsd:date) Declaration(NamedIndividual(:Ivan)) ClassAssertion(:Person :Ivan) DataPropertyAssertion(:bornOnDate :Ivan "2006-04-14"^^xsd:date) ObjectPropertyAssertion(:hasChild :Martin :Ivan) ObjectPropertyAssertion(:hasChild :Lenka :Ivan)
The ontology also defines some rules:

(Please note that in Protege 4.1 the SWRL rules editor is broken, so these rules were not created in Protege, they were written in a text editor by directly editing the ontology source code. The ontology swrl_tutorial.owl is written in functional syntax that Protege 4.1 can load directly.)
There is a small inconvenience when working with SWRL rules, that their human syntax is not well standardized. The image above is a screenshot from the Protege 4.1, which renders the rules in a variant of Manchester syntax without namespace qualifiers.
The rule in the listing displayed as
Person(?x), hasChild min 1 Person(?x) -> Parent(?x)is in the functional syntax (defined in A Syntax for Rules in OWL2) written as
DLSafeRule(
Annotation(rdfs:comment "Rule with class expression")
Body(
ClassAtom( :Person Variable(var:x) )
ClassAtom(
ObjectMinCardinality( 1 :hasChild :Person )
Variable(var:x)
)
)
Head(
ClassAtom( :Parent Variable(var:x) )
)
)
Its meaning is that individuals, that are in the Person class, and that have at least one property hasChild with an individual from the class Person, must then be in the Parent class. Or in another words, that persons with at least one child are parents.
When you use the Pellet reasoner, which supports SWRL rules, it will infer that Martin and Lenka are in the class Parent, as can be seen
on the following image in the lower right corner:
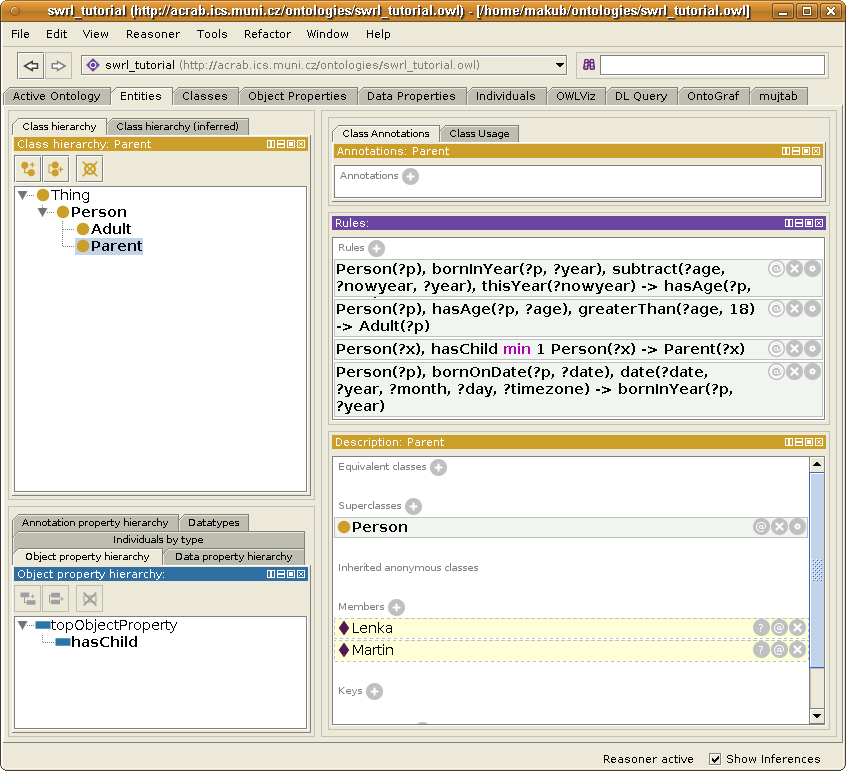
When you click on the question mark (?) on right of the inferred information, the reasoner even provides information how that information was inferred:
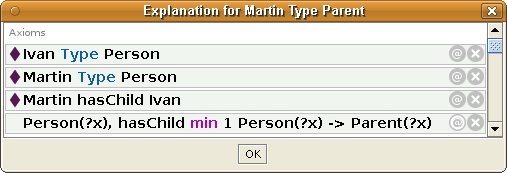
Please note that you can always create a new named class equivalent to a class expression, and use the named class instead of the class expression.
Also note that in this particular example, there is no need to use a SWRL rule, the same can be modeled simply by setting the Parent class as subclass of the "(hasChild min 1 Person)" class expression in OWL. Or by making it equivalent to the class expression, which is a stronger assertion. SWRL rules are really needed only for modeling non-tree structures which cannot be modeled in OWL.
Person(?p), integer[>= 18 , <= 65](?age), hasAge(?p, ?age) -> hasDriverAge(?p, true)The data range restriction is satisfied when the ?age variable has an integer value between 18 and 65 inclusive.
This example shows a complex data range restriction with facets,
a simpler example would be integer(?x) or xsd:date(?y) which restrict the type without using facets.
For a full descrition of data ranges see OWL 2 Data Ranges. An example data range using union, intersection, complement and facets in the same time would be in Manchester syntax:
((integer[>=1,<=2] or integer[>5,<7]) and not ({0}))(?y)
and the same in funtional syntax:
DataRangeAtom(
DataIntersectionOf(
DataUnionOf(
DatatypeRestriction( xsd:integer xsd:minInclusive "1"^^xsd:integer xsd:maxInclusive "2"^^xsd:integer )
DatatypeRestriction( xsd:integer xsd:minExclusive "5"^^xsd:integer xsd:maxExclusive "7"^^xsd:integer )
)
DataComplementOf(
DataOneOf( "0"^^xsd:integer )
)
)
Variable(var:y)
)
The following rules from the listing use the core built-ins, they would be most correctly written as:
Person(?p), hasAge(?p, ?age), swrlb:greaterThan(?age, 18) -> Adult(?p) Person(?p), bornOnDate(?p, ?date), xsd:date(?date), swrlb:date(?date, ?year, ?month, ?day, ?timezone) -> bornInYear(?p, ?year)The first of these two rules says that persons who have age higher than 18 are adults. The second rule takes the data value of the bornOnDate property, which must be of xsd:date type, splits it into pieces, and adds the year part as the value of the bornInYear property for the same person.
When the reasoner is used, the second rule is used:
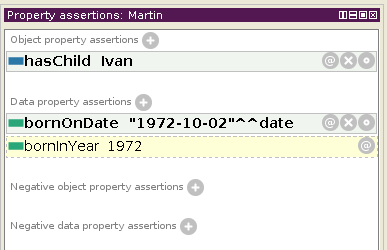
There are some restrictions in the use of built-ins. In the Pellet reasoner, they can be used only in the body of a rule, not in the head. And they can be used only for data values, not for object values. Some built-ins, like the swrlb:date(), can be used with both bound and unbound variables, while other, like the swrlb:greaterThan(), can be used only for bound variables.
Thanks to the How to extend Pellet2.2.2′s SWRL rule support with your custom built-in ? page I have found how to define my own custom built-ins for use with OWL API 3.
The rule
Person(?p), bornInYear(?p, ?year), my:thisYear(?nowyear), swrlb:subtract(?age, ?nowyear, ?year) -> hasAge(?p, ?age)uses the my:thisYear custom built-in to bind the integer value of the current year to the ?nowyear variable, and then uses the swrlb:subtract core built-in to compute the person's age in years, then it sets the result as the value of the hasAge property. The rule can be used in a Java program:
package cz.makub; import aterm.ATermAppl; import com.clarkparsia.pellet.owlapiv3.PelletReasonerFactory; import com.clarkparsia.pellet.rules.builtins.BuiltInRegistry; import com.clarkparsia.pellet.rules.builtins.GeneralFunction; import com.clarkparsia.pellet.rules.builtins.GeneralFunctionBuiltIn; import org.mindswap.pellet.ABox; import org.mindswap.pellet.Literal; import org.mindswap.pellet.utils.ATermUtils; import org.semanticweb.owlapi.apibinding.OWLManager; import org.semanticweb.owlapi.io.OWLObjectRenderer; import org.semanticweb.owlapi.model.*; import org.semanticweb.owlapi.reasoner.OWLReasoner; import org.semanticweb.owlapi.reasoner.OWLReasonerFactory; import org.semanticweb.owlapi.reasoner.SimpleConfiguration; import org.semanticweb.owlapi.vocab.PrefixOWLOntologyFormat; import uk.ac.manchester.cs.owlapi.dlsyntax.DLSyntaxObjectRenderer; import java.text.SimpleDateFormat; import java.util.Calendar; import java.util.Map; import java.util.Set; import static org.mindswap.pellet.utils.Namespaces.XSD; /** * Example of Pellet custom SWRL built-in. * * Run in Maven with <code>mvn exec:java -Dexec.mainClass=cz.makub.SWRLBuiltInsTutorial</code> * * @author Martin Kuba makub@ics.muni.cz */ public class SWRLBuiltInsTutorial { /** * Implementation of a SWRL custom built-in. */ private static class ThisYear implements GeneralFunction { public boolean apply(ABox abox, Literal[] args) { Calendar calendar = Calendar.getInstance(); String year = new SimpleDateFormat("yyyy").format(calendar.getTime()); if (args[0] == null) { //variable not bound, fill it with the current year args[0] = abox.addLiteral(ATermUtils.makeTypedLiteral(year, XSD + "integer")); return args[0] != null; } else { //variable is bound, compare its value with the current year return year.equals(args[0].getLexicalValue()); } } public boolean isApplicable(boolean[] boundPositions) { //the built-in is applicable for one argument only return boundPositions.length == 1; } } private static final String DOC_URL = "http://acrab.ics.muni.cz/ontologies/swrl_tutorial.owl"; public static void main(String[] args) throws OWLOntologyCreationException { //register my built-in BuiltInRegistry.instance.registerBuiltIn("urn:makub:builtIn#thisYear", new GeneralFunctionBuiltIn(new ThisYear())); //initialize ontology and reasoner OWLOntologyManager manager = OWLManager.createOWLOntologyManager(); OWLOntology ontology = manager.loadOntologyFromOntologyDocument(IRI.create(DOC_URL)); OWLReasonerFactory reasonerFactory = PelletReasonerFactory.getInstance(); OWLReasoner reasoner = reasonerFactory.createReasoner(ontology, new SimpleConfiguration()); OWLDataFactory factory = manager.getOWLDataFactory(); PrefixOWLOntologyFormat pm = manager.getOntologyFormat(ontology).asPrefixOWLOntologyFormat(); //use the rule with the built-in to infer data property values OWLNamedIndividual martin = factory.getOWLNamedIndividual(":Martin", pm); listAllDataPropertyValues(martin,ontology,reasoner); OWLNamedIndividual ivan = factory.getOWLNamedIndividual(":Ivan", pm); listAllDataPropertyValues(ivan,ontology,reasoner); } public static void listAllDataPropertyValues(OWLNamedIndividual individual,OWLOntology ontology,OWLReasoner reasoner) { OWLObjectRenderer renderer = new DLSyntaxObjectRenderer(); Map<OWLDataPropertyExpression, Set<OWLLiteral>> assertedValues = individual.getDataPropertyValues(ontology); for (OWLDataProperty dataProp : ontology.getDataPropertiesInSignature(true)) { for (OWLLiteral literal : reasoner.getDataPropertyValues(individual, dataProp)) { Set<OWLLiteral> literalSet = assertedValues.get(dataProp); boolean asserted = (literalSet!=null&&literalSet.contains(literal)); System.out.println((asserted ? "asserted" : "inferred") + " data property for "+renderer.render(individual)+" : " + renderer.render(dataProp) + " -> " + renderer.render(literal)); } } } }The program when run prints the inferred values for the bornInYear, hasAge and hasDriverAge properties:
asserted data property for Martin : bornOnDate -> 1972-10-02 inferred data property for Martin : hasAge -> 39 inferred data property for Martin : bornInYear -> 1972 inferred data property for Martin : hasDriverAge -> true asserted data property for Ivan : bornOnDate -> 2006-04-14 inferred data property for Ivan : hasAge -> 5 inferred data property for Ivan : bornInYear -> 2006Please note that the rules worked in cooperation. First the rule with the core built-in computed the integer value of the bornInYear property, then the rule with the custom built-in computed the integer value of the hasAge property, and at last the rule with the faceted data range assigned the boolean value of the hasDriverAge property. Unfortunately I do not know if it is possible to use the custom built-in inside of Protege 4.1.
The SWRL specification allows only data values as arguments for built-ins. However the Pellet reasoner is
able to process rules with builtins that work with individuals. Just there is no documentation for that. The only information
available is from an email by Brandon Ibach
and the poorly documented source of the classes in the com.clarkparsia.pellet.rules.builtins package.
I have created a class CustomSWRLBuiltin.java that is similar to the Pellet's GeneralFunctionBuiltIn class,
but allows also individuals, not only literals. It provides an interface CustomSWRLFunction that should be
implemented to provide a built-in that can accept both literals and individuals.
An example of a built-in that works with individuals is a built-in that takes as input an individual and a separator string, obtains the IRI of the individual, splits the IRI into two parts at the position of the separator string, and binds these two IRI parts into variables:
package cz.makub; import cz.makub.swrl.CustomSWRLBuiltin; import com.clarkparsia.pellet.owlapiv3.PelletReasonerFactory; import com.clarkparsia.pellet.rules.builtins.BuiltInRegistry; import org.mindswap.pellet.ABox; import org.mindswap.pellet.Node; import org.mindswap.pellet.utils.ATermUtils; import org.semanticweb.owlapi.apibinding.OWLManager; import org.semanticweb.owlapi.io.OWLObjectRenderer; import org.semanticweb.owlapi.model.*; import org.semanticweb.owlapi.reasoner.OWLReasoner; import org.semanticweb.owlapi.reasoner.OWLReasonerFactory; import org.semanticweb.owlapi.reasoner.SimpleConfiguration; import org.semanticweb.owlapi.vocab.PrefixOWLOntologyFormat; import uk.ac.manchester.cs.owlapi.dlsyntax.DLSyntaxObjectRenderer; import java.util.Map; import java.util.Set; import static org.mindswap.pellet.utils.Namespaces.XSD; /** * Example of a Pellet SWRL built-in that works with both Individuals and data literals. * * Run in Maven with <code>mvn exec:java -Dexec.mainClass=cz.makub.IndividualSWRLBuiltinTutorial</code> * * @author Martin Kuba makub@ics.muni.cz */ public class IndividualSWRLBuiltinTutorial { /** * The built-in implementation. */ public static class IRIparts implements CustomSWRLBuiltin.CustomSWRLFunction { @Override public boolean isApplicable(boolean[] boundPositions) { //applicable only to 4 arguments, two bound and two unbound return boundPositions.length == 4 && boundPositions[0] && boundPositions[1] && !boundPositions[2] && !boundPositions[3]; } @Override public boolean apply(ABox abox, Node[] args) { //accepts IRIparts(individual,separator string,unbound variable,unbound variable) if (!args[0].isIndividual() || !args[1].isLiteral() || args[2] != null || args[3] != null) return false; //get the IRI of the individual in the first argument String iri = args[0].getNameStr(); //get the string value of the second argument String separator = ATermUtils.getLiteralValue(args[1].getTerm()); //split the IRI at the separator int idx = iri.indexOf(separator); if (idx == -1) return false; String prefix = iri.substring(0, idx); String id = iri.substring(idx + separator.length()); //bind the third and fourth arguments to the IRI parts args[2] = abox.addLiteral(ATermUtils.makeTypedLiteral(prefix, XSD + "string")); args[3] = abox.addLiteral(ATermUtils.makeTypedLiteral(id, XSD + "string")); return true; } } //a simple example ontology private static final String DOC_URL = "http://acrab.ics.muni.cz/ontologies/swrl_tutorial_ind.owl"; public static void main(String[] args) throws OWLOntologyCreationException { //register my built-in implementation BuiltInRegistry.instance.registerBuiltIn("urn:makub:builtIn#IRIparts", new CustomSWRLBuiltin(new IRIparts())); //initialize ontology and reasoner OWLOntologyManager manager = OWLManager.createOWLOntologyManager(); OWLOntology ontology = manager.loadOntologyFromOntologyDocument(IRI.create(DOC_URL)); OWLReasonerFactory reasonerFactory = PelletReasonerFactory.getInstance(); OWLReasoner reasoner = reasonerFactory.createReasoner(ontology, new SimpleConfiguration()); OWLDataFactory factory = manager.getOWLDataFactory(); PrefixOWLOntologyFormat pm = (PrefixOWLOntologyFormat) manager.getOntologyFormat(ontology); //print the SWRL rule listSWRLRules(ontology, pm); //use the rule with the built-in to infer property values OWLNamedIndividual martin = factory.getOWLNamedIndividual(":Martin", pm); listAllDataPropertyValues(martin, ontology, reasoner); } public static void listSWRLRules(OWLOntology ontology, PrefixOWLOntologyFormat pm) { OWLObjectRenderer renderer = new DLSyntaxObjectRenderer(); for (SWRLRule rule : ontology.getAxioms(AxiomType.SWRL_RULE)) { System.out.println(renderer.render(rule)); } } public static void listAllDataPropertyValues(OWLNamedIndividual individual, OWLOntology ontology, OWLReasoner reasoner) { OWLObjectRenderer renderer = new DLSyntaxObjectRenderer(); Map<OWLDataPropertyExpression, Set<OWLLiteral>> assertedValues = individual.getDataPropertyValues(ontology); for (OWLDataProperty dataProp : ontology.getDataPropertiesInSignature(true)) { for (OWLLiteral literal : reasoner.getDataPropertyValues(individual, dataProp)) { Set<OWLLiteral> literalSet = assertedValues.get(dataProp); boolean asserted = (literalSet != null && literalSet.contains(literal)); System.out.println((asserted ? "asserted" : "inferred") + " data property for " + renderer.render(individual) + " : " + renderer.render(dataProp) + " -> " + renderer.render(literal)); } } } }The ontology contains just an individual and the following rule that uses the custom built-in
IRIparts
in its body to split the IRI of each person at the point of the # character. In the head, the rule has two
data property assertions just to use the produced string values:
Person(?p), IRIparts(?p,"#"^^xsd:string,?q,?r) -> hasIRIprefix(?p, ?q), hasIRIid(?p, ?r)
When run, the program should print:
hasIRIid(?p, ?r) ⋀ hasIRIprefix(?p, ?q) ← Person(?p) ⋀ urn:makub:builtIn#IRIparts((?p) , (#) , (?q) , (?r)) inferred data property for Martin : hasIRIprefix -> http://acrab.ics.muni.cz/ontologies/swrl_tutorial_ind.owl inferred data property for Martin : hasIRIid -> Martin
Here I collect my findings from working with OWL+SWRL ontologies.
A surprising feature of OWL properties are their domain and ranges. For those who undertook some course in mathematics, the behavior is counter-intuitive. If you define a property domain in OWL, it is not a constraint on the individuals that may appear as the property's source. Instead, it forces any individual which has this property to belong to the domain.
For example, let's define a property olderThan with domain Person, and assert Martin olderThan Lenka. Then either by mistake or because it is tempting to reuse the property, we assert Pyramids olderThan The_Great_Wall_of_China. Instead of an incosistent ontology we get a result that Pyramids are a Person.
This counter-intuitive behavior of OWL properies is mentioned in OWL 2 Primer,chapter 4.8 Datatypes, it is better to think about property domains and ranges in the way suggested in 4.6 Domain and Range Restrictions, i.e. as adding implicit additional information, e.g. that every individual in the range of a :hasWife property must be a woman.
A reflexive relation in mathematics is a binary relation on a set for which every element is related to itself. One would expect that the reflexive property in OWL 2 does the same on its domain. However it's not the case. A reflexive relation in OWL 2 makes every individual related to itself, its domain is owl:Thing. If you define a domain for a reflexive property, you force the domain to be equivalent to owl:Thing. The reason is the definition of ReflexiveObjectProperty semantics, which says
∀ x : x ∈ ΔI implies ( x , x ) ∈ (OPE)OP
where ΔI is "object domain", not the property domain.
What you need to do instead is to define the reflexivity only on the domain. If you look up the Reflexive Object Properties definition, you may notice that it is just a shortcut for
SubClassOf( owl:Thing ObjectHasSelf( OPE ) ). So we can do the same for any class other than owl:Thing.
Thus we may define for example that only roles are equalTo themselves:
SubClassOf( :Role ObjectHasSelf( :equalTo ) )
NegativeObjectPropertyAssertion( :hasSpouse :Martin :Peter) NegativeDataPropertyAssertion( :hasEmail :Martin "president@whitehouse.gov")if you want to express that an individual does not belong to a class, you have to express it as that the individual belongs to the complement of the class:
ClassAssertion( ObjectComplementOf( :BadGuy ) :Martin )Even more difficult is to express a "closed" world, because OWL has the "Open World Assumption". For example, if you assert that "Bob has licence for Matlab", OWA says that there may be other people with the licence, just we do not know who they are. So if you want to express that only Bob has a licence for Matlab, you can express it as (in Manchester and functional syntaxes):
Person and (not ({Bob})) EquivalentTo hasLicence max 0 ({Matlab})
EquivalentClasses(
Annotation(rdfs:comment "Only Bob has a licence for Matlab")
ObjectMaxCardinality( 0 :hasLicence ObjectOneOf(:Matlab) )
ObjectIntersectionOf( ObjectComplementOf(ObjectOneOf(:Bob)) :Person )
)
which is saying "Persons other than Bob have at most zero licences for Matlab". The ObjectOneOf() class expression, which
defines a class by enumerating all its members, is the only way how to close the world.
If you want to have a rule with a negation of a property, you can also do it with cardinality restriction (in Manchester and functional syntaxes):
Person(?p),(locatedIn max 0 Room)(?p) -> PersonNotInRoom(?p)
DLSafeRule(
Body(
ClassAtom( :Person Variable(var:p) )
ClassAtom( ObjectMaxCardinality( 0 :locatedIn :Room ) Variable(var:p) )
)
Head(
ClassAtom( :PersonNotInRoom Variable(var:p) )
)
)
Sometimes one needs to model a relation that represents partial ordering. There are no primitives for that in OWL 2, but partial ordering relation can be modelled by creating a property that is reflexive, transitive and antisymmetric.
An example of such property is the property :greaterOrEqual from the ontology poset.owl
that is visualised on the following image:
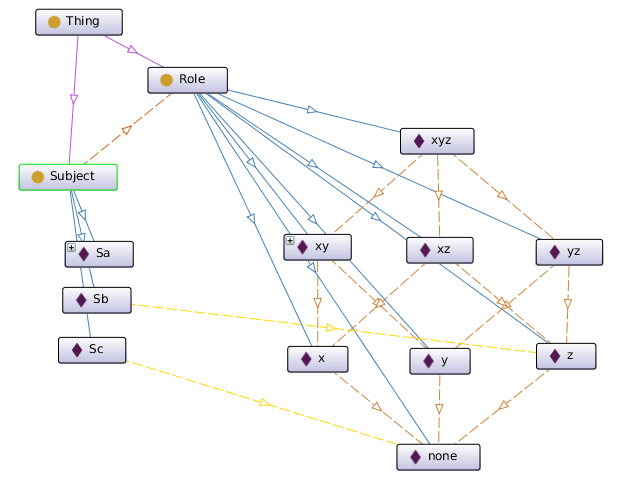
The trick is in creating a property :greaterOrEqual that has two subproperties - :equalTo that is symmetric and :greaterThan that is transitive:
Declaration(ObjectProperty(:equalTo)) Declaration(ObjectProperty(:greateOrEqual)) Declaration(ObjectProperty(:greaterThan)) SubClassOf(:Role ObjectHasSelf(:equalTo)) TransitiveObjectProperty(:greaterThan) SubObjectPropertyOf(:equalTo :greateOrEqual) SubObjectPropertyOf(:greaterThan :greateOrEqual)
In knowing a technology, it may be helpful to know where its limits are. In OWL 2 and SWRL, the limits are imposed mainly by the underlaying logic.
I assume that you have heard about mathematical logic, at least about propositional logic and first order predicate logic.
To refresh your memory, propositional logic is the logic whose formulae are made of atomic propositions like A, B, having always one of the values true or false, and logical connectives like negation (¬A), and (A∧B), or (A∨B) and implication (A→B). Propositional logic is sound (only deriving correct results), complete (able to derive any logically valid formula) and decidable (the algorithms for deciding whether a formula is valid end in finite time).
Predicate logic is the logic which adds predicates (like P(x,y)) which represent relations, i.e. produce true or false for a combination of values of the terms x and y; quantifiers: existential ∃ ("there exists") and universal ∀ ("for all"); and terms made of variables and functions, like f(x), g(y,z). Thus predicate logic can form formulas like ∀x∃y(P(x)→Q(f(y))).
First order predicate logic is the logic where the quantifiers can range only over elements of sets. In higher order logics, quantifiers can range over sets, functions and other objects. So, for example, the sentence that "every set of real numbers has a minimum" cannot be expresed in first order logic, because the quantification ranges over sets, not set elements.
First order predicate logic is sound and complete, however it is not decidable. It is semidecidable, valid formulas can be proven, but non-valid formulas may need infinite time to construct a counter-example of infinite size.
There are known algorithms that can prove valid theorems in first order predicate logic, namely the tableaux algorithm, however if the theorem is not valid, the algorithm may not end in finite time.
The OWL language is based on description logics (DL) , which is a family of logics designed to be as expressive as possible while retaining decidability. The OWL version 1 is based on the description logic SHOIN(D), and OWL version 2 is based on the DL SROIQ(D).
The OWL 2 DL is a decidable fragment of first order predicate logic, with some decidable extensions that go beyond first order logic (see Relationship with other logic for details).
It is known that OWL 1 cannot express the uncle relation, which is a chain of relations parent and sibling. OWL 2 can express uncle using property chains, however it still cannot express relations between individuals referenced by properties. Namely OWL 2 cannot express the child of married parents concept because it cannot express the relationship between parents of the individual (see A better uncle for OWL article).
Using SWRL, we can express even the child of married parents concept. However arbitrary SWRL rules would lead to undecidability, so only so-called DL-safe rules are implemented in reasoners. DL-safe rules are rules applied only to named individuals, they do not apply to individuals that are not named but are known to exist. See What are DL-Safe SWRL Rules? for details.
Being a fragment of first order predicate logic, the DL cannot express the following: